本次分享的论文被收录于 2014 年的 USENIX Security。第一作者 Yarom 在侧信道攻击领域有很多精彩的作品。今天要介绍的 FLUSH+RELOAD 攻击是其中有代表性的一篇。这篇文章发表至今已经有近八年，其中一些技术细节已经过时，但是它可以作为一个绝妙的 demo 来展示侧信道攻击的思路，这些思路至今依然没有过时。

作为学术文章，原文中只对学术界最关心的核心问题进行了阐述。为了更完整地讲解整个故事，我会对原文省略的步骤做一些补充。

背景介绍

侧信道攻击（Side-Channel Attack）是一种十分有魅力的攻击。传统的攻击（比如memory corruption）多是逻辑上的漏洞，而侧信道攻击一般利用程序运行的时间、环境（电磁场、温度等）等反推机密信息。侧信道攻击主要针对的是计算机安全领域 CIA（Confidentiality, Integrity and Availability）中的 C ，比如通过程序执行时间长短来窃取秘钥等信息。侧信道漏洞分为软件漏洞和硬件漏洞，其中后者威胁更为强大，因为一旦硬件被部署，就无法根除，最多只能从软件上做一些方法来限制、减弱这些攻击的威力。

Trusted Execution Environment （可信执行环境， TEE）是一种依赖硬件隔离手段来保护程序运行的技术。随着 TEE 技术的发展，传统的 memory corruption 类型的漏洞威胁程度逐渐被降低，而侧信道攻击则逐渐引起人们的重视，因为一个硬件上的侧信道漏洞就可能足以导致整个 TEE 被攻破。至今针对不同平台的 TEE （Intel 的 SGX， Arm 的 TrustZone，AMD 的 SEV等）都已经有很多侧信道攻击工作。

本文介绍的侧信道攻击 FLUSH+RELOAD 利用的是硬件中的三级缓存 （L3 Cache），通过测量访问时间来获取秘钥信息，属于侧信道攻击中的 Cache Timing Attack。

攻击思路

RSA 算法简要回顾

【Reminder：不喜欢数学的可以跳过这一段】RSA 是目前主流的加密算法之一，它的安全性依赖大数分解问题的复杂程度。大数分解问题即给定 $n=pq$（其中 $p$ 和 $q$ 是两个大素数）后，很难由 $n$ 求出 $p$ 和 $q$ 的值。在 RSA 中，我们还要选定一个公共的指数 $e$，比如在 GnuPG 的实现中，$e$ 的值默认为 65537。随后由 $(n,e)$ 作为公钥，$(p,q,d)$ 作为私钥，其中 $$ d\equiv e^{-1}\mod ((p-1)(q-1)). $$ 而 RSA 具体实现中，有一些常见的优化，首先可以用中国余数定理把 $d$ 分成 $d_p\equiv d\mod(p-1)$ 和 $d_q\equiv d\mod(q-1)$ 两个部分。对密文 $c$ 的解密也将分为 $m_p \equiv c^{d_p} \mod p$ 和 $m_q \equiv c^{d_q} \mod q$ 两个部分。最后使用 Garner’s Formula $$ \begin{aligned} h&=(m_p-m_q)(q^{-1}\mod p)\mod p,\\ m&=m_q+hq \end{aligned} $$ 复原密文 $m$。值得注意的是，对 $d_p$ 或者 $d_q$ 其一的破解即可破解整个秘钥。

如果你碰巧没看到上面那段话，你只需要知道解密过程中需要计算： $$ m\equiv c^d\mod p, $$ 其中私钥 $d$ 是算法的关键，也是我们攻击的目标。

RSA 实现中的快速幂

由于 $d$ 是个很大的数字，计算 $c^d$ 的具体实现中会使用快速幂来优化效率。快速幂的思路是，我们把 $d$ 按二进制表示成 $$ d=2^{k-1}d_{k-1}+\cdots+2^0d_0, $$ 因此 $$ c^d=c^{\sum_i2^id_i}=\prod_{i=0}^{k-1}c^{2^id_i}=\prod_{d_i=1}c^{2^i}. $$ 于是我们可以使用 Square-and-Multiply 的方法来计算 $c^d$，伪代码如下：

bigint exp_mod(c,d,p)
{
	bigint x = 1;
	for (int i = k - 1; i >= 0; i--) {
		x = x * x; // square
		x = x % p; // reduce
		if (d[i] == 1) { // d[i] are the bits of number d
			x = x * c; // multiply
			x = x % p; // reduce
		}
	}
	return x;
}

快速幂带来的隐患

这段非常常见的快速幂算法其实给侧信道攻击提供了可能。在循环体每一次执行中，如果 d[i] 的值是 0，那么该次执行流程是 Square-Reduce；如果 d[i] 是 1，那么执行流程是 Square-Reduce-Multiply-Reduce。因此，私钥 $d$ 的全部信息被包含在了程序运行的 control flow 中。也就是说，如果我们能想办法 trace 整个程序的执行，那么就有办法从程序的 control flow 中 recover 私钥 $d$，即观察每次循环中，Multiply-Reduce 部分的代码是否被执行。

一些操作系统知识的回顾

我们假设攻击者只是一个普通的进程，那么他显然没办法随意地观测其他进程的执行。而这就是 Cache Timing Attack 的用武之地了。

在介绍具体的攻击方式之前，我们先回忆一些操作系统的基础知识。首先，系统中进程是资源分配的单元，每个进程有自己的虚拟地址空间，有自己的一系列文件描述符。其次，当多个进程打开同一个文件时，系统会用 Copy-on-Write (COW) 的方式透明地让它们 share 同一个文件。也就是说，当文件从磁盘加载到内存后，如果文件始终没有被修改，那么无论多少进程打开了它，在内存中都只有一份共享的物理页，这些页被映射到进程各自的虚拟地址空间。直到某个进程对文件内容进行了修改，系统才会复制该页，再修改进程的映射，让其访问到新的物理页，而其他进程继续共享原有未被修改的物理页。COW 的过程逻辑上对所有进程是透明的，即理论上进程自己感知不到资源被与其他进程共享了。最后，当代系统支持动态链接库：静态链接的程序会在自己内部包含所有代码，这会导致二进制文件很大，而动态链接可以让每个二进制文件只包含自己独立的部分，动态链接库的部分在运行时被链接器装载到进程里。

说到文件操作，我们熟悉的往往是自己写代码时手动打开的文件，比如写个简单的程序，在 main 里调用 open 等函数。但实际上进程会自动打开一些文件，比如动态链接库。动态链接库本质上是一些二进制文件，当一个进程需要某个库时，这个库对应的二进制文件会被装载到进程的栈和堆中间的 gap 里的某个位置（这个 gap 对于 64-bit 系统来说是巨大的），而这个装载过程也同样是 COW 的。与普通的二进制文件一样，动态链接库也有自己的 .text 段用来储存代码，有自己的 .data 段用来储存初始化的全局变量等。而 .text 段多数情况下是不会被修改的，因此在 COW 机制下，多个进程一般会 share 用于保存 .text段的物理页。而全局变量被修改时，则会触发 COW，此后拥有一部分自己的 .data 页。

加密服务一般会作为动态链接库安装在某个系统文件夹中，比如你敲完 apt install gnupg 之后，GnuPG 就被安装到了某个文件夹中。也就是说，根据我们刚刚的讨论，加密库的 .text 段大部分情况下会被进程之间共享！

尽管 COW 机制中的共享在理论上对进程是透明的，但是实际上狡猾的进程却有办法感知并利用这个机制。我们假设一个 victim 进程正在进行某次解密操作，而另一个 spy 进程试图窃取 victim 进程使用的私钥。attacker 让 spy 进程中链接了与 victim 相同的加密库。现在按照我们的预期， spy 和 victim 将会共享这个加密库 .text 段的物理页。

打破透明的工具：L3 Cache

我们已经逐渐接触到了攻击的核心，现在还差最后一片背景知识：什么是 Cache ？什么是 L3 Cache ？

Cache（缓存）是提升计算机性能的重要部件。说白了 Cache 其实就是一堆寄存器，放在内存条和 CPU 中间，CPU 访问过的内存会被存在 Cache 里，近期再次访问相同的地址就会直接在 Cache 中操作（包括读和写），当 Cache 塞满了则会驱逐最老的条目，并对应更新内存条里的内容（这里是最 naive 的理解，多核 CPU 还需要考虑 cache coherence 的问题）。寄存器比较贵，所以一般 Cache 不会很大。如果把刚刚讨论的 Cache 再看成内存，我们可以套娃式地再加入一层 Cache，这层 Cache 比刚刚的更快，但是也更小。

文章中讨论了 Intel Core i5-3470 处理器的 Cache 结构，为了充分利用内存访问的 locality，这款四核处理器有三个级别的 Cache。其中 L1 Cache 分成 32kB data cache 和 32kB instruction cache，L2 Cache 是 256kB 的统一 Cache，既可以存 data 也可以存 instruction。每个核都有一份自己的 L1 和 L2 Cache。而 6MB 的 L3 Cache 则是四个核共有的。Cache Line 是 Cache 的基本单元，这款处理器中 Cache Line 的大小是 64B。

此外这款处理器的 Cache 是 Inclusive 的，即存在于 L1、 L2 中的 Cache Line，一定也存在于 L3 中。而对 L3 中 Cache Line 的驱逐，一定也会导致 L1、L2 中对应的 Cache Line 被驱逐。

除了被动地填充、驱逐，Intel 还提供了一些主动进行 Cache 操作的指令，这主要是为多核同步而提供的。比如 clflush 0(addr) 指令，可以用于主动驱逐 addr 对应的 Cache Line。然而，clflush 是一个非特权指令，所有进程都可以随意地执行它。

（这里其实隐藏了一个问题，进程所看到的的地址是虚拟地址，这里的 addr 也就是虚拟地址。每个进程中虚拟地址可以完全不一样，这是否会影响 Cache 索引？可能直观上我们会觉得 Cache 只负责加速内存到核的数据转移，而地址转换是核内的事情， 因此不会影响，但是实际上 Cache 中虚拟地址是有作用的。当代主流的处理器 Cache 一般采用 VIPT(Virtually Indexed Physically Tagged) 的方式进行索引，详情可以看这篇短文。结论是虚拟地址不会影响我们的攻击，clflush 依然会把对应的 Cache Line 驱逐。）

如何 trace 进程的执行？

现在我们万事俱备，可以回到开头提出的问题了：如何 trace victim 进程的执行？如果我们完成了 trace，就可以从 control flow 中恢复私钥。有了铺垫以后，思路其实非常简单：spy 进程对时间切片，每个时间片内首先驱逐核心代码段的 Cache Line （FLUSH），比如 exp_mod 中的 Multiply、Square 和 Reduce，在时间片末尾再次访问这些地址（RELOAD），并记录访问的时间。如果这个时间很短，那么说明这段时间内，victim 进程执行了该段代码，反之，如果这个时间很长，说明这段时间内没有执行这段代码。由于我们针对的是所有核共享的 L3 Cache，所以不需要担心进程被 schedule 到不同的核上。

时间片的长度要比一次循环体执行小很多，这样可以更清楚地观察程序执行，即攻击的 Resolution 更高。但是如果一个时间片长度过小，会导致 FLUSH 和 RELOAD 本身的操作在时间片内的比重增大，而如果 victim 的访问操作和 RELOAD 重叠，就会无法成功探测这次执行。因此时间片的长度既不能太小也不能太大。

攻击结果

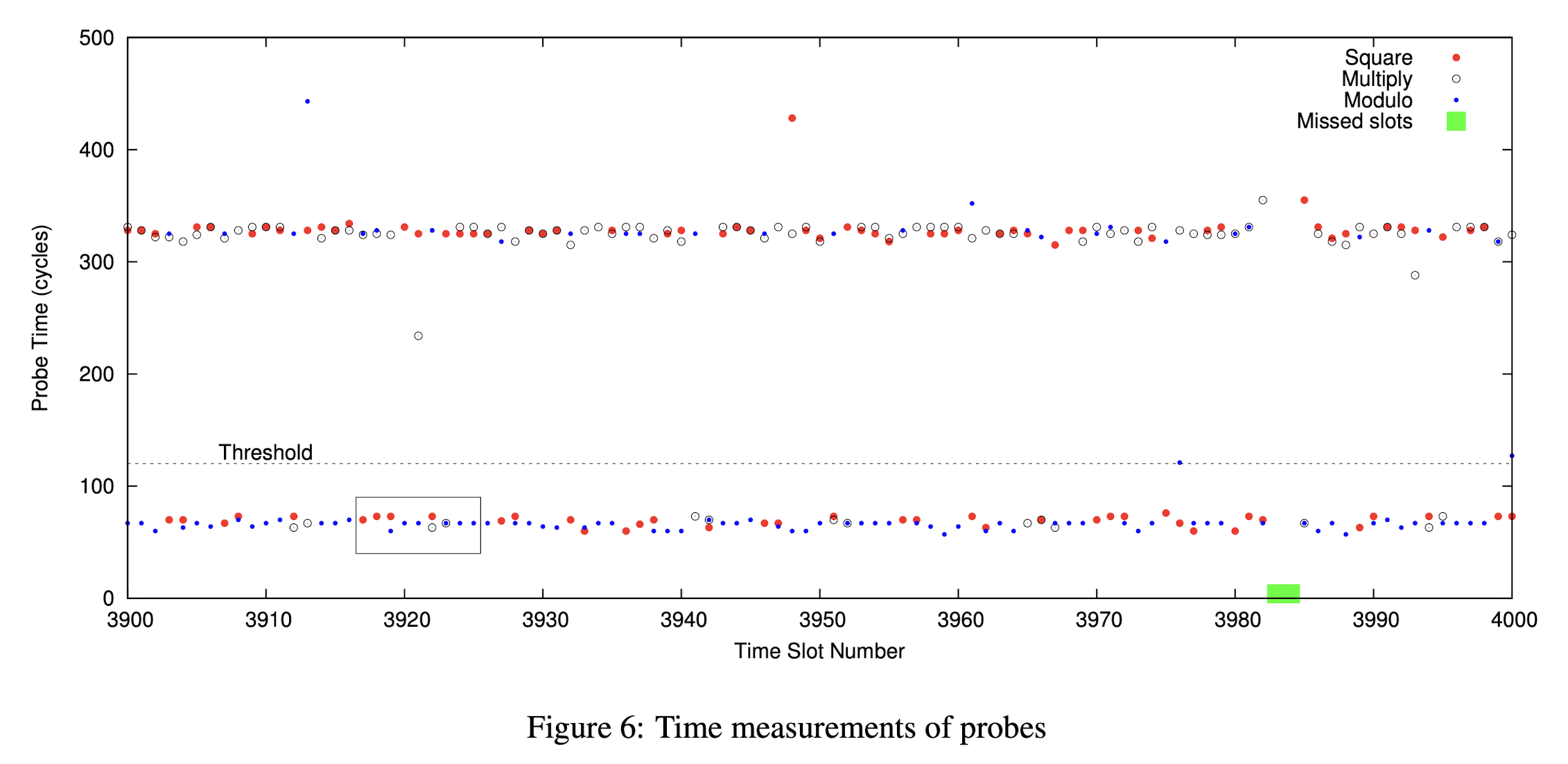
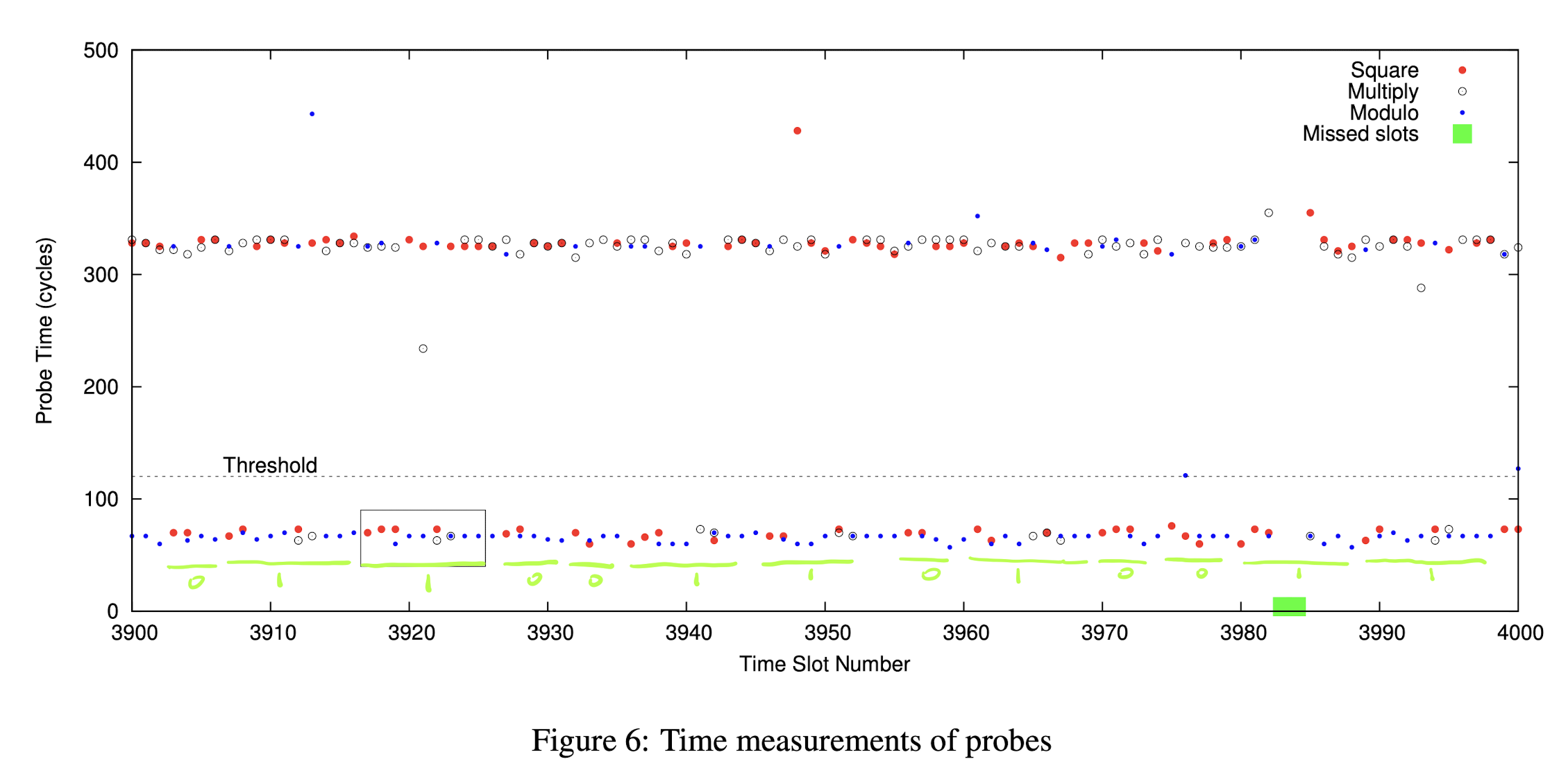
这里先直接放出原文中的测量结果图：

第一眼看上去一定感觉眼花缭乱，甚至想直接关闭这个页面再也不看第二眼。但是实际上稍微理解之后，这幅图里的信息是十分清楚的。图中每一个横坐标对应一个时间片，在一个时间片内，我们会关注 Multiply、Square 和两次 Reduce 是否被执行。Square 对应红点，Multiply 对应白点，Reduce 对应蓝点。纵轴代表 RELOAD 操作需要的时间。如果一个点比较高，说明对应的操作这段时间没有被执行，如果点比较低，说明这段时间内对应的操作被执行了。

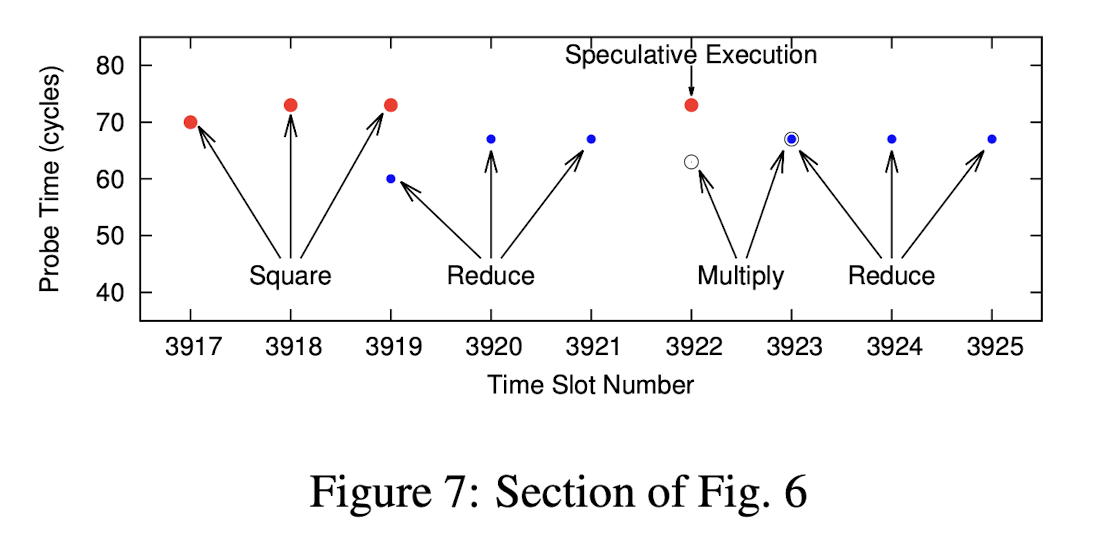
首先我们先关注图里的黑框部分，这部分原文做了详细说明：

图中可以看到明显的一次 Square-Reduce-Multiply-Reduce 操作。因此对应的私钥 bit 应该是 1。大家可以尝试按类似的方式去分析 Figure 6，看看得到的 bit 串结果是什么，再查看下面的答案。我抱着试一试，不太可能全对的心态尝试了一下后，发现和原文给出的答案一模一样：

End of the Story? No

回顾一下至此我们得到了什么：一串私钥的 bits。理论情况下我们已经得到私钥了。但是实际操作中一定会因为系统 schedule、RELOAD overlaps with victim access、分支预测（刚刚图中其实有分支预测的迹象）等等导致 bits 的错误。但是秘钥是精确的，差一个 bit 都不能让我们成功解密密文。那么我们得到的东西毫无价值吗？当然不是。

RSA 问题复杂是因为暴力搜索答案的搜索空间过大。但是现在我们手上已经有一个接近于答案的 bit 串了，我们只需要在这个 quasi-key 附近的空间进行搜索，就可以很快搜索到答案。原文中只给出了一个比值：不同的算法依赖的准确 bit 数量不一样，范围在 27%~70%。也就是说，我们只需要精准拿到 70% 的 bits，就可以破解私钥了。

经过我自己的了解，这些算法一般是 Lattice algorithm。一个 Lattice 可以脑补成若干基向量的整数倍叠加后能到达的点的集合（严格来说是一个 $\mathbb{Z}^n$ 上的自由模）。在这样的 Lattice 里找最接近（欧氏距离）一个给定点的向量是一个很复杂的问题（因为这里的“若干”可以相当大）。这个问题等价于在 Lattice 中最接近原点的向量。一般可以使用 Lenstra–Lenstra–Lovász（LLL，Lattice 版本的 Schmidt 正交化）算法进行 basis reduction，从而求解最接近原点的向量。

攻击的拓展

这里讨论两个攻击的拓展。

第一个是原文中进行了实验验证的 cross virtual machine 的攻击。原理是当代服务器一般会采用 content aware page sharing 机制。意思是，服务器会主动探索是否有内容相同的物理页，有的话就进行合并。这对云服务器是很有必要的。比如一个服务器跑了 100 个 Ubuntu 16.04 的虚拟机，想必有一大部分物理页是重复的，而采用这种方式，只需保留一份。而这种共享也给跨虚拟机攻击提供了可能。

第二个是从其他论文中了解到，快速幂操作不止在 RSA 中使用。在基于椭圆曲线的 ECC 中，求解 $$ a=kb,a,b\in Curve,k\in\mathbb{F} $$ 的数乘结果时，可以把 Square-and-Multiply 变换为 Double-and-Add，本质上也是一种快速幂操作。因此一些 ECC 库也会收到侧信道的威胁。

如何防御？

如果想根除这种侧信道漏洞，必须修改硬件。第一条思路是让 clflush 成为特权指令，只有操作系统或者 Hypervisor 才有权利执行。第二条思路是给 Cache 加上 Owner Process 的 Tag，一个 Process 只允许驱逐自己的 Cache Line。第二条思路在很多近期 RISC-V 平台的工作中已经实现。

软件上也可以进行一些治标不治本的防范。思路分为预防、监察两种。预防是指在写加密库的时候，就考虑到侧信道的威胁，实现 “constant-time algorithm”。目前已知的 BoringSSL 等加密库就是如此。第二种是让系统监察 spy process 的异常行为，比如频繁 flush cache，如果检查到就强制关闭进程等。

这里还有一条有意思的小知识：秘钥不是越长越安全。刚刚我们提到了攻击中时间片不能太长或者太短。这个太短是有一个下限的：即一次 FLUSH+RELOAD 而完全不等待所需要的时间。如果一个循环体小于这个时间，那么这个攻击就无法达到足够的粒度，而减小秘钥长度可以做到这一点。反之，如果你的秘钥被设置得足够长，它将在侧信道攻击面前毫无抵抗能力，攻击者可以达到任意想要的精度。这一观点在 Walter 的论文中被讨论：Longer keys may facilitate side channel attacks.

结语

本文介绍了一种 Cache Timing Attack。侧信道攻击的种类繁多，远远不止这种攻击。Security 领域往往有优化和安全之间的 trade-off，而每当硬件或者软件上采取了一种优化时，都可以考虑这种优化会不会导致一些安全隐患。比如针对 TLB 的 TLBleed 侧信道攻击、针对分支预测的大名鼎鼎的 Spectre 攻击等等。由于这篇短文完成时间过短，我并没有来得及手动复现文章中的攻击，希望后续我可以补上。如果有本文相关的问题，欢迎联系我一起讨论。